殘差一定要降到1e-03以下才代表收斂嗎？【轉發】

2017-08-15 by:CAE仿真在線來源:互聯網

太長不看版

判斷收斂不僅要看殘差,而且要使用monitor來監測計算結果隨迭代次數的變化情況。另一種方法是使用雙精度求解器:當采用單精度求解器算到殘差不再下降的時候,采用雙精度求解器繼續計算,如果殘差能繼續顯著下降,那就說明計算是收斂的,否則就說明計算不收斂。

總所周知FLUENT的默認收斂標準是殘差降低到1e-03以下(能量方程和P-1方程除外,這兩個方程的默認收斂標準是1e-06)。但是,殘差降低到1e-03以下和收斂是否有必然聯系呢?換句話說,殘差不能降到1e-03以下,是否意味著不收斂?

先看兩個例子。

例1:三維方腔突擴突縮流動

這是公眾號先前的文章“為何我這個流動總是算不收斂?我要砸電腦!”中的例子。如圖1所示,一個邊長為2m的立方體連接著兩根方形截面的管子。入口流速是1m/s,流體的密度是1kg/m3,粘性系數是10-5Pa?s。以入口流速為特征速度,入口截面的邊長為特征長度,則流動雷諾數為105,所以流態是湍流流動。坐標原點位于立方體的中心,坐標軸的方向如圖所示。使用FLUENT中的基于壓力的求解器計算,速度和壓力的耦合(Pressure-Velocity Coupling)采用SIMPLE算法,湍流模型使用k-ω SST。入口使用velocity-inlet邊界條件,流速按上述條件設置。入口的湍流參數設為:湍流強度=5%,水力直徑=1m。出口使用pressure-outlet邊界條件,回流的湍流參數設為與入口相同。計算前的初始流場按照入口邊界的數值初始化。

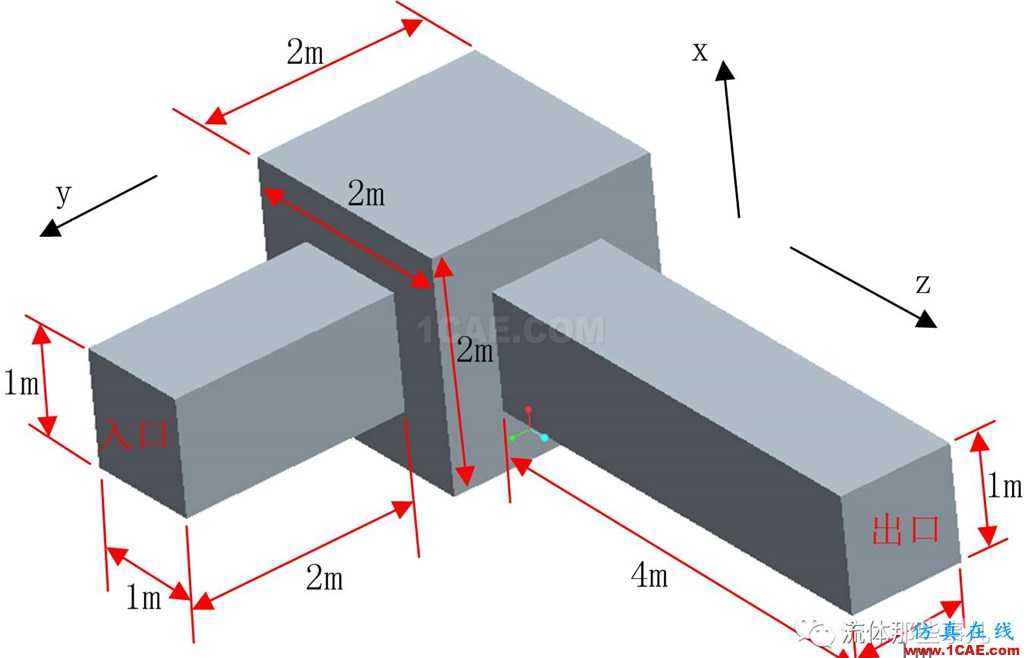
圖1 例1

用定常算法(Steady)來計算,發現迭代500次之后,各方程的殘差都開始振蕩,在1e-02和1e-03之間徘徊,不再下降;特別是k方程和ω方程的殘差,從來未曾下降到1e-03以下(圖2)。

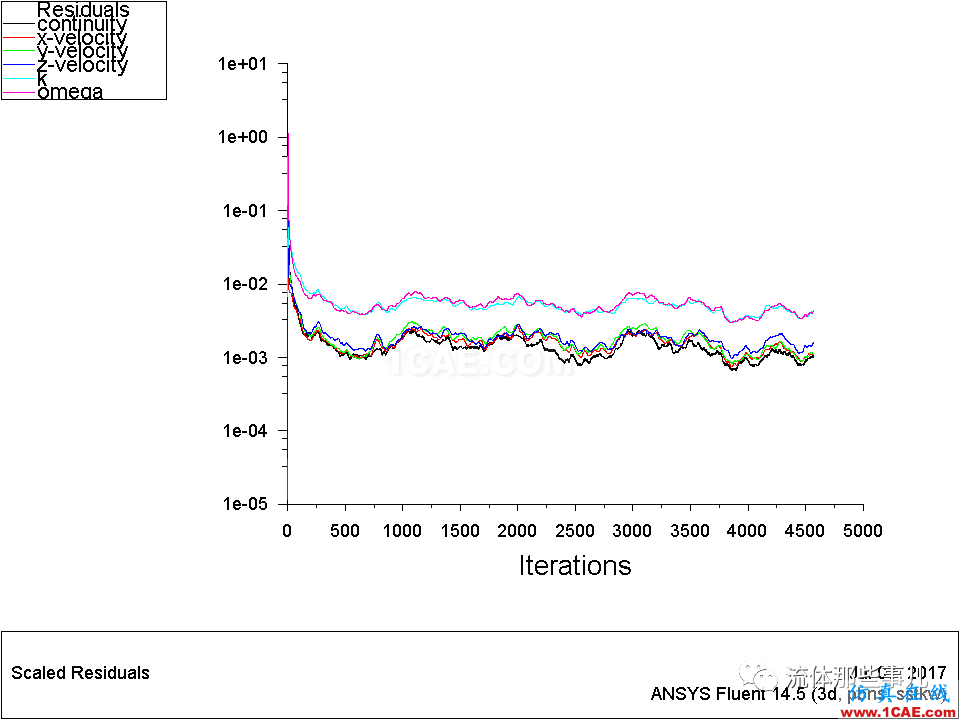
圖2 例1——殘差曲線

使用monitor監測點(-0.5,0.5,0.5)處的流速隨迭代次數的變化情況,其曲線振蕩得非常厲害(圖3)。所以顯然這個題沒有收斂。

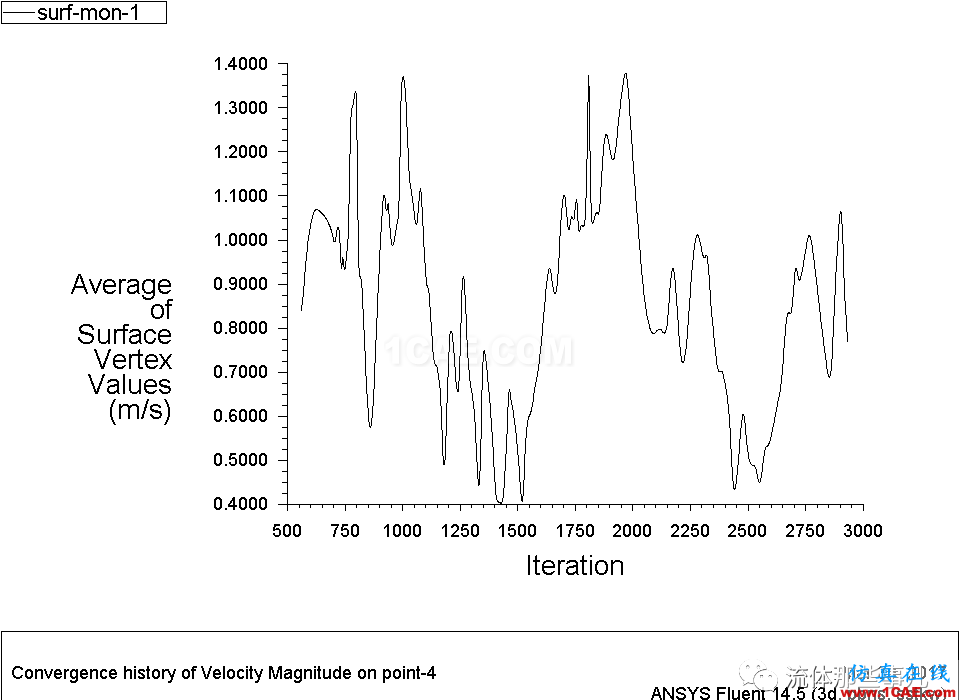
圖3 例1——(-0.5,0.5,0.5)處的速度隨迭代次數的變化情況

例2:圓管內的湍流流動

空氣(密度=1.225kg/m3,粘性系數=1.7894×10-5Pa?s)流過一根直徑為0.03m,長度為2.4m的圓管,使用二維軸對稱模型計算,入口使用速度入口(velocity-inlet)條件,參數設為:流速=10m/s,湍流強度=5%,水力直徑=0.03m,出口使用壓力出口(pressure-outlet)條件。使用基于壓力的求解器,算法為SIMPLE,湍流模型采用標準k-ε模型。計算前的初始流場按照入口邊界的數值初始化。

圖4 例2——管道入口附近的網格

殘差曲線如圖5所示。可以看出,雖然其它幾個方程的殘差都降到很低,但是連續方程的殘差降低到2e-2左右就不再下降了。

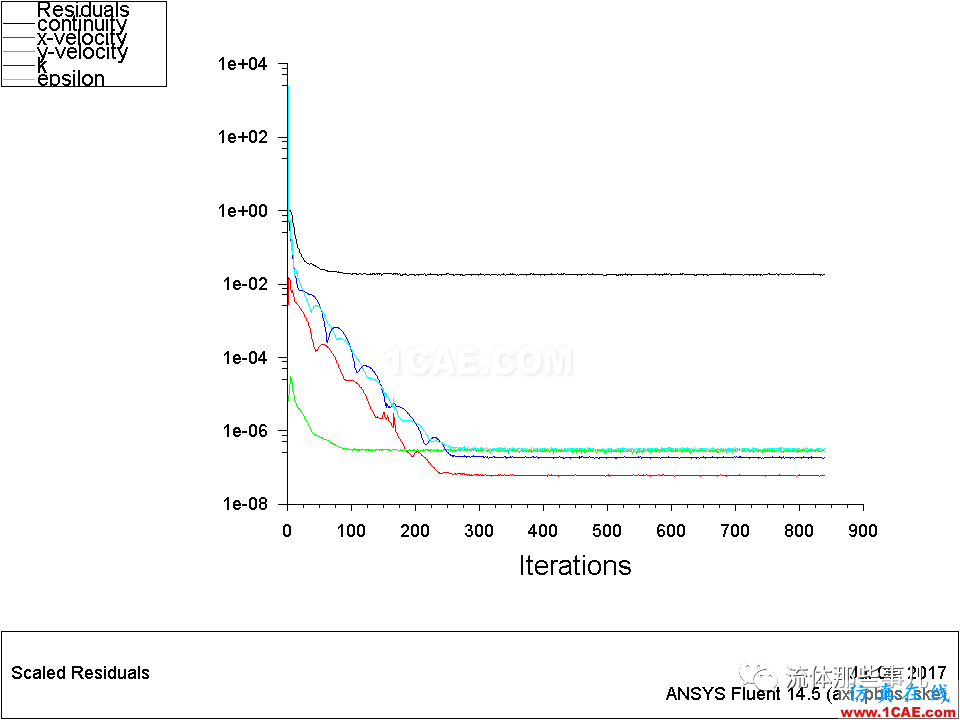
圖5 例2——殘差曲線

但是,如果我們使用monitor監測流場的變化情況,可以發現隨著迭代次數的增加,流場并沒有發生變化(圖6-圖9),所以這個題是收斂的。

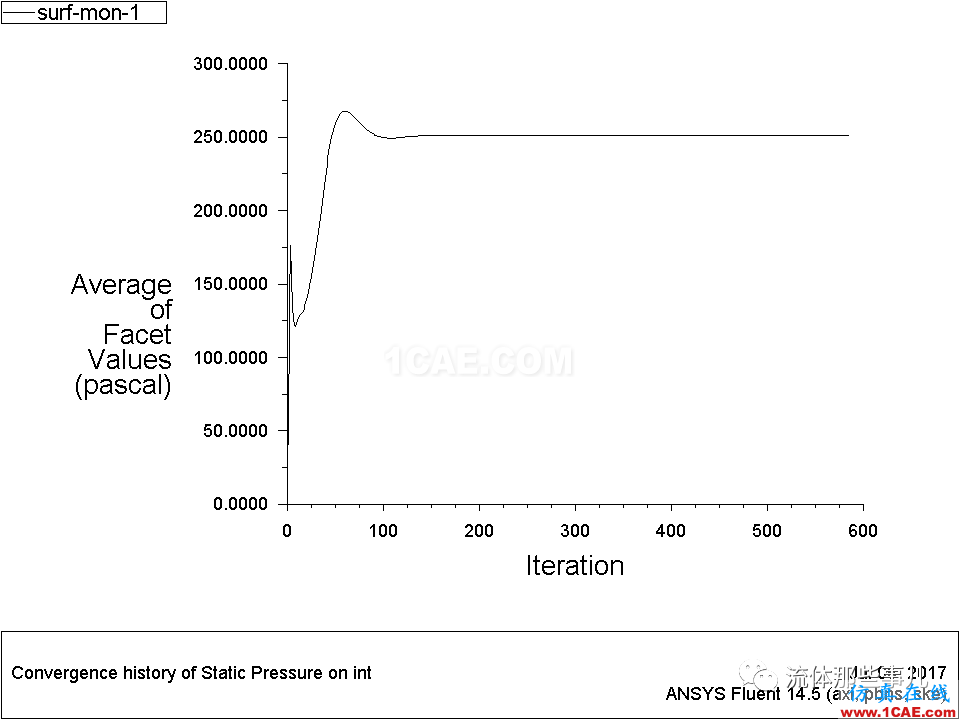
圖6 例2——管道入口壓力隨迭代次數的變化

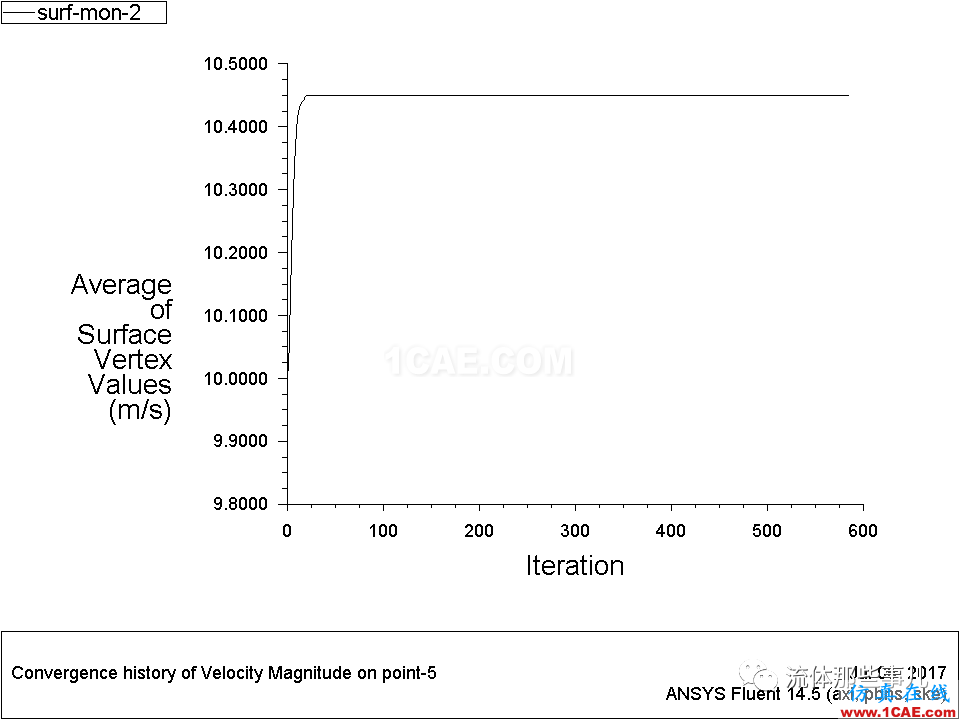
圖7 例2——管道入口附近某個點的速度隨迭代次數的變化

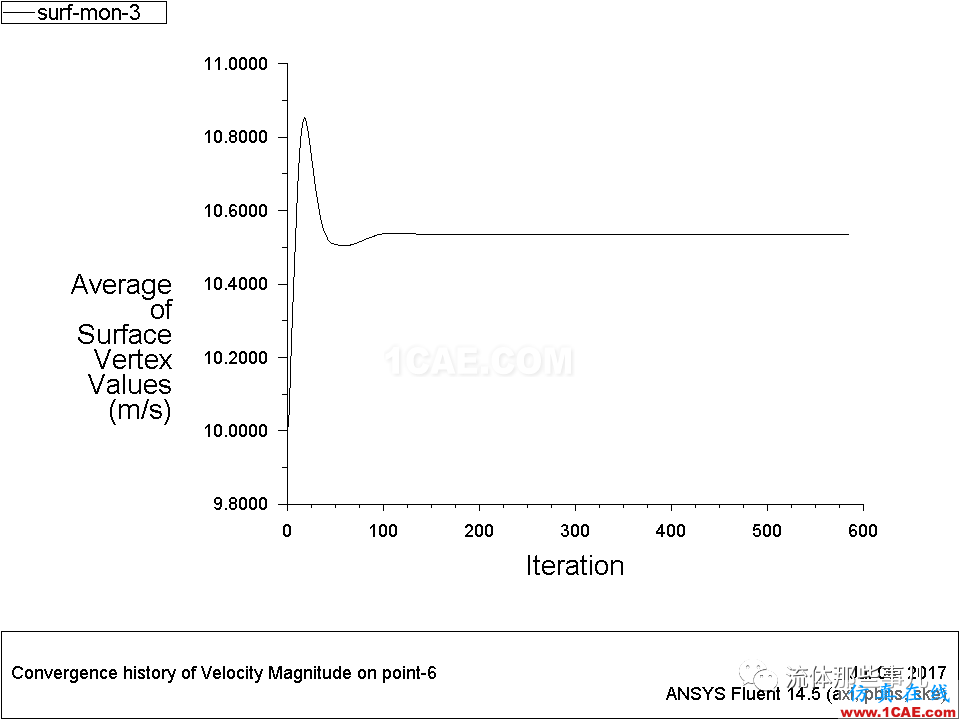
圖8 例2——管道中部某個點的速度隨迭代次數的變化

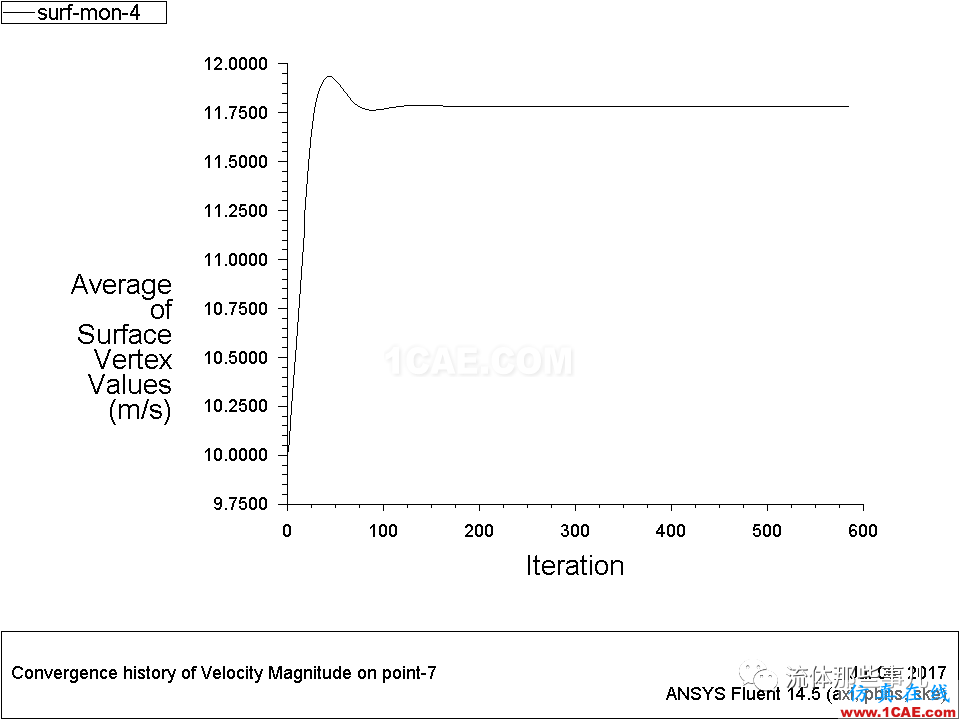
圖9 例2——管道出口附近某個點的速度隨迭代次數的變化

從這兩個例子可以看出,并不能用殘差是否能降低到1e-03以下來判斷收斂。其實,在FLUENT的User’s Guide [1]中“Judging Convergence”這一節中,也指出了判斷收斂不僅要看殘差,而且要使用monitor來監測計算結果隨迭代次數的變化情況。要弄清這個問題,需要知道FLUENT是怎樣計算殘差的,關于這方面的內容在FLUENT User’sGuide中“Definitionof Residuals for the Pressure-Based Solver”和“Definition of Residuals for the Density-Based Solver”中有介紹。例如,FLUENT的基于壓力的求解器在計算連續方程的殘差的時候,會將每次迭代的殘差都除以最初5次迭代的殘差,然后才顯示到殘差曲線圖上。因此,如果用戶在迭代之前設定的初始條件已經比較接近實際的流場,那么最初5次迭代的殘差就會比較小,這樣的話殘差曲線上顯示出來的數值就會比較大(這正是例2中發生的情況)。

用FLUENT計算一個題,如果已經計算到殘差不再下降了,這時判斷是否收斂的一種方法是采用monitor監測計算結果隨迭代次數的變化情況。此外還有一種方法,那就是改用雙精度(double-precision)求解器。例如,對于上面的兩個例子,如果我們分別改用雙精度求解器來計算,那么將得到圖10、圖11所示的殘差曲線。可以看出,對于例1,改用雙精度求解器之后,殘差沒有顯著變化;而對于例2,改用雙精度求解器之后,連續方程的殘差可以降低到1e-08以下。注意,這里對每個題都采用雙精度求解器從頭開始計算,其實在實際的計算中,可以將單精度求解器計算的結果導入到雙精度求解器中繼續計算。

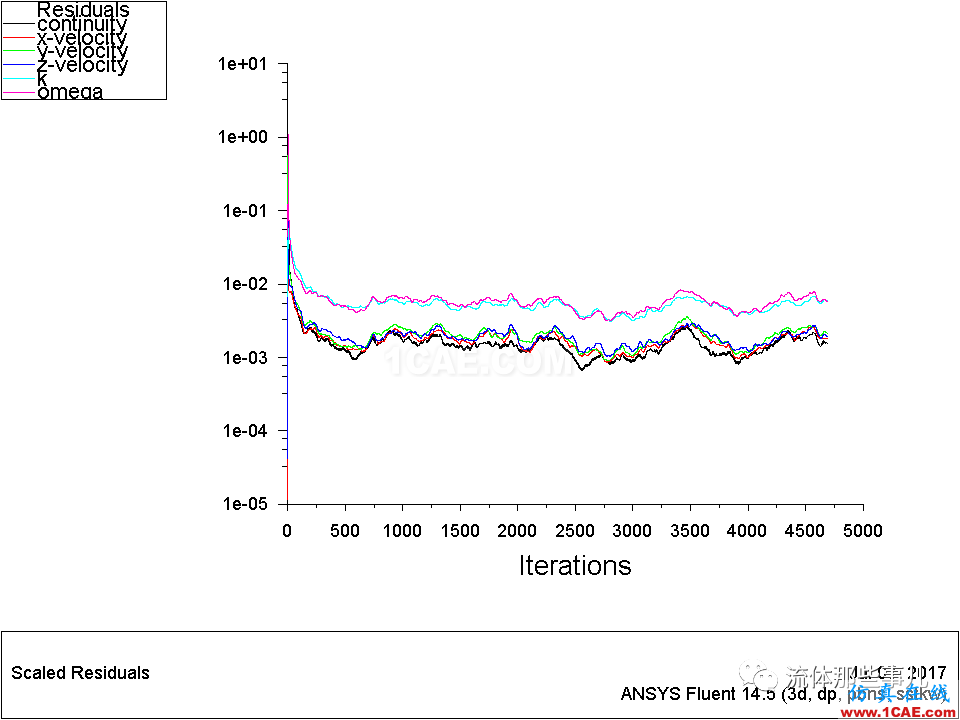
圖10 例1——殘差曲線。雙精度求解器。

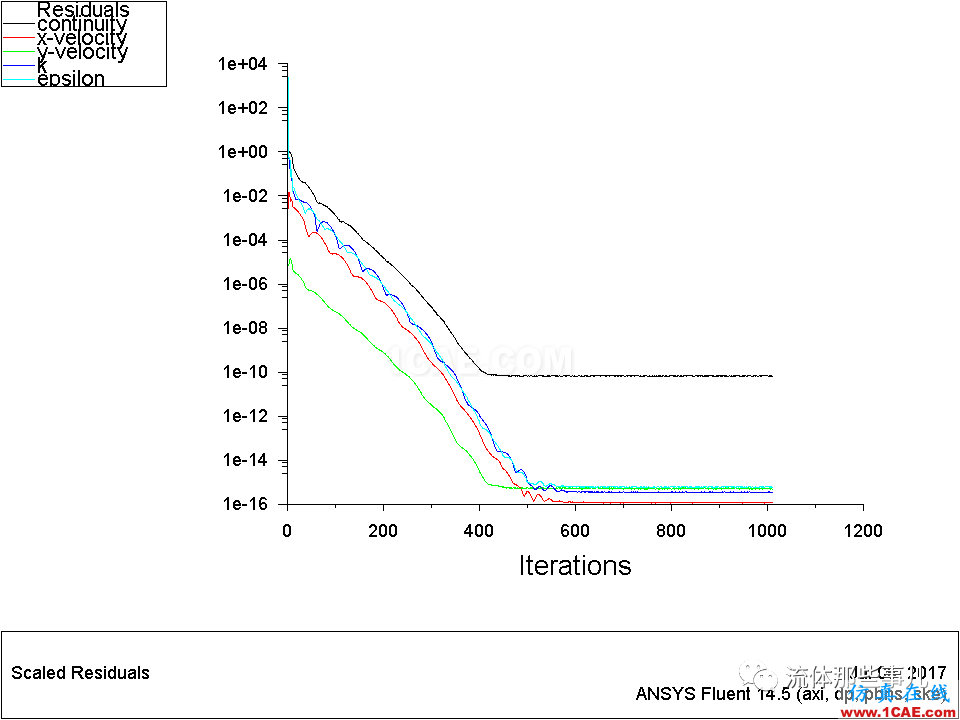
圖11 例2——殘差曲線。雙精度求解器。

也就是說,計算一個題,當采用單精度求解器算到殘差不再下降的時候,采用雙精度求解器繼續計算,如果殘差能繼續顯著下降,那就說明計算是收斂的,否則就說明計算不收斂。這其中的道理其實很簡單。殘差不能下降的原因有兩種,一種是因為計算誤差已經降低到機器精度,而另一種則是因為設置不當導致計算不收斂(例如使用定常的求解器計算具有強烈的非定常分離的流動)。單精度求解器是使用單精度浮點數計算的,其機器精度大約有7位有效數字;而雙精度求解器是使用雙精度浮點數計算的,其機器精度大約有16位有效數字。因此,如果殘差不能降低是機器精度導致的,那么改用雙精度求解器之后殘差可以繼續顯著降低。反之,如果殘差不能降低是計算不收斂導致的,那么改用雙精度求解器是無濟于事的。

作者感謝北京航空航天大學宇航學院的研究生張少卿和馮盛;他們提供了例2的素材。另外,北航宇航學院的研究生衣然閱讀了本文的初稿并提出了很好的建議。

轉自公眾號: 流體那些事兒葉漢玉

開放分享：優質有限元技術文章,助你自學成才