圓柱繞流，你真的會算嗎？【轉發】

2017-05-01 by:CAE仿真在線來源:互聯網

圓柱繞流是流體力學中的經典問題。幾乎所有的流體力學教科書在講解不可壓縮無旋流動(勢流)的時候,都以圓柱繞流為例分析平行流、偶極子以及點渦的組合。圓柱繞流的實際應用也非常廣泛,例如橋墩、煙囪、架空電纜、換熱器中的管束、飛機起落架等等。

圓柱繞流的幾何形狀看似簡單,但是其流動圖像隨著雷諾數(Re=ρUD/μ,其中ρ為流體密度,U為來流速度,D為圓柱直徑,μ為流體的動力粘性系數)的變化非常豐富,至今還有許多機理并未被人們認識清楚。圖1是不同Re數下的圓柱繞流圖像。圖2是圓柱繞流阻力系數(CD=2F/ρU2A,其中F為阻力,A為迎風面積。迎風面積等于圓柱的直徑乘以圓柱的長度)隨Re數的變化情況。

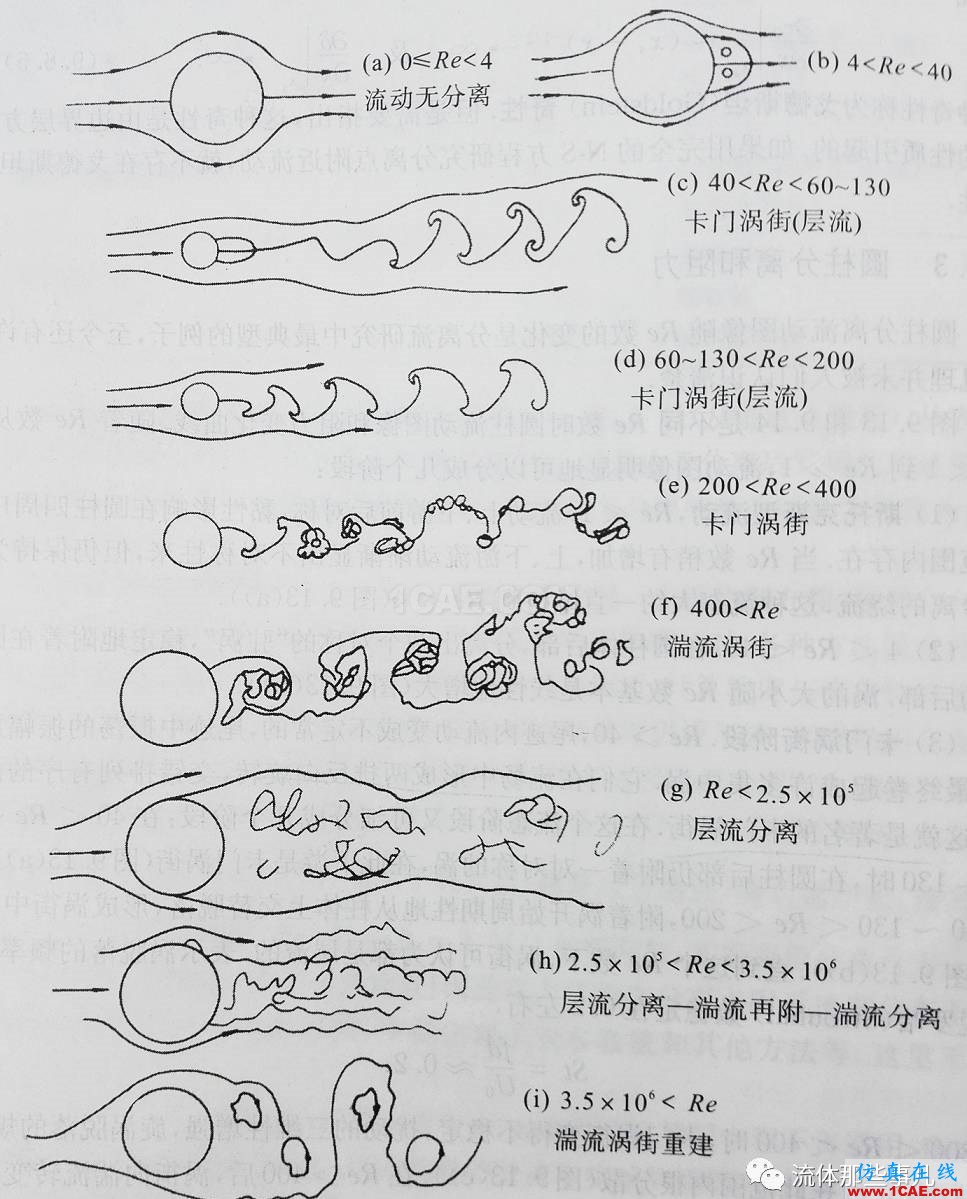
圖1 不同Re數下的圓柱繞流圖像。(復制自文獻[1])

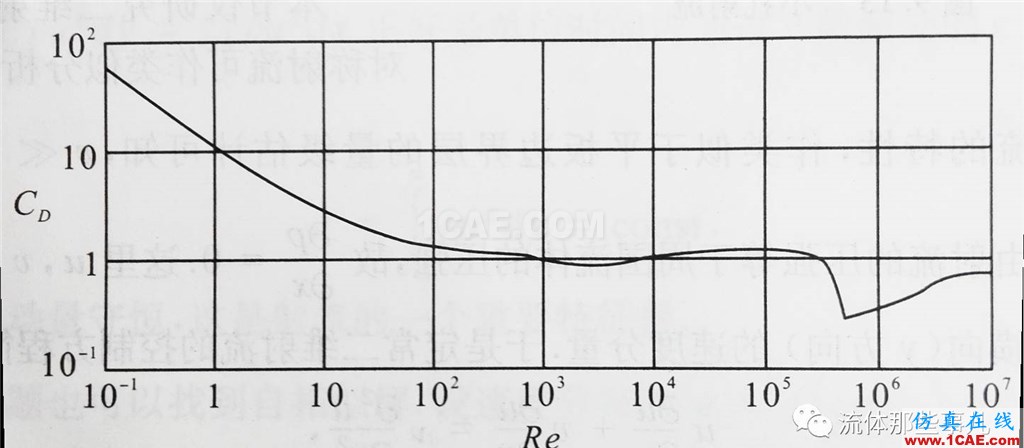
圖2 圓柱繞流阻力系數隨Re數的變化。實驗結果。(復制自文獻[1])

由于流動的復雜性,圓柱繞流的數值模擬是非常具有挑戰性的課題。在最近出版的一本流體力學教科書[2]中,作者展示了圓柱繞流模擬的三個案例。使用的程序是商業軟件FLUENT,模擬的雷諾數分別是150,104和107。使用二維求解器計算;由于圓柱的幾何對稱性,將計算域設定為一個半圓形區域(圖3);使用了三種不同密度的網格:粗網格(徑向30×圓周方向60)、中等網格(60×120)以及細網格(120×240)。圖4是中等網格的局部放大圖。三個雷諾數下都使用定常算法求解。

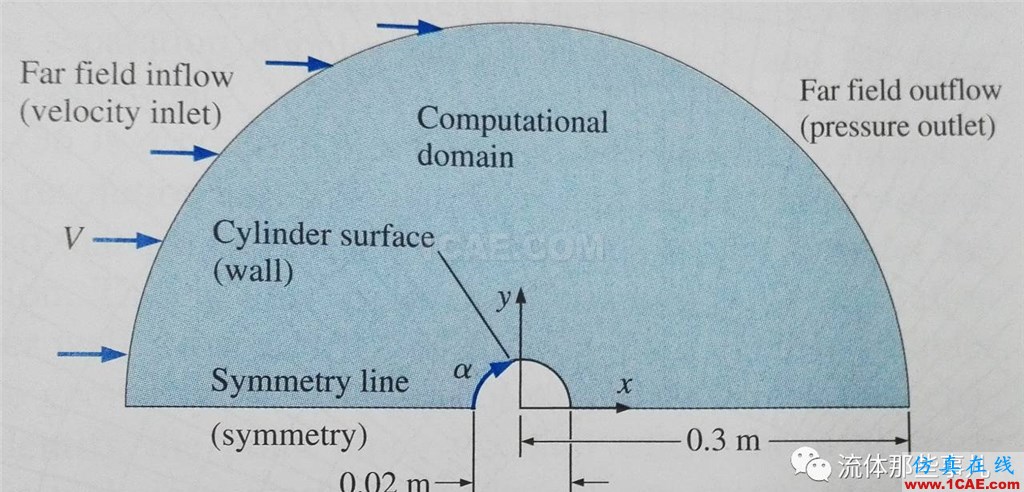
圖3 計算域(復制自文獻[2])

圖4 中等網格(復制自文獻[2])

當Re=150時,對于實驗測得的阻力系數,不同文獻的結果有一定差異,范圍在1.1~1.4之間。實驗表明這時圓柱表面的邊界層是層流的,分離點位于82°的位置(圖5(a)),即位于圓柱最高點的前方;尾跡也是層流的。

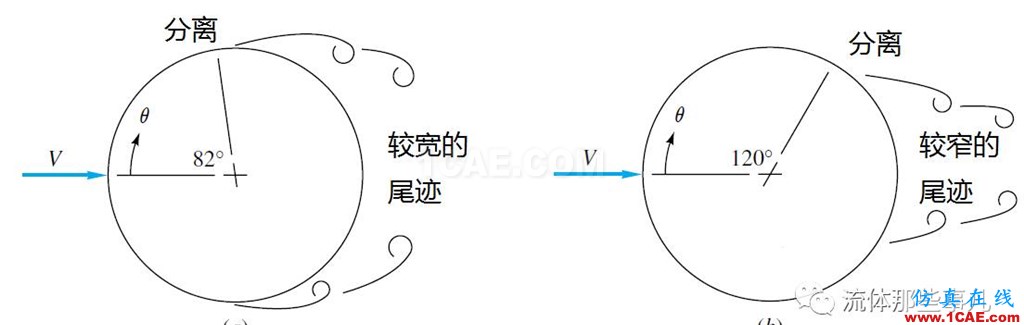
圖5 分離點的位置。(a) Re=150和104; (b) Re=107

對Re=150使用層流模型計算。圖6是三種不同密度網格的計算結果(流線圖);三種密度的網格的計算收斂性都很好。對于圖6(a)的粗網格的結果,邊界層的分離點位于圓柱最高點的后方,在120°的位置,阻力系數為1.00。對于圖6(b)的中等網格的計算結果,分離點稍向上游移動,位于110°的位置,似乎和實驗接近了一點,但是算出的阻力系數卻降低到0.982——與實驗值的距離更遠了。對于圖6(c)的細網格的結果,外觀上與中等網格的結果差異不大,分離點位于109°的位置,而阻力系數更小(0.977)。再加密網格,結果的變化就非常小了,因此可以認為已經達到網格無關。

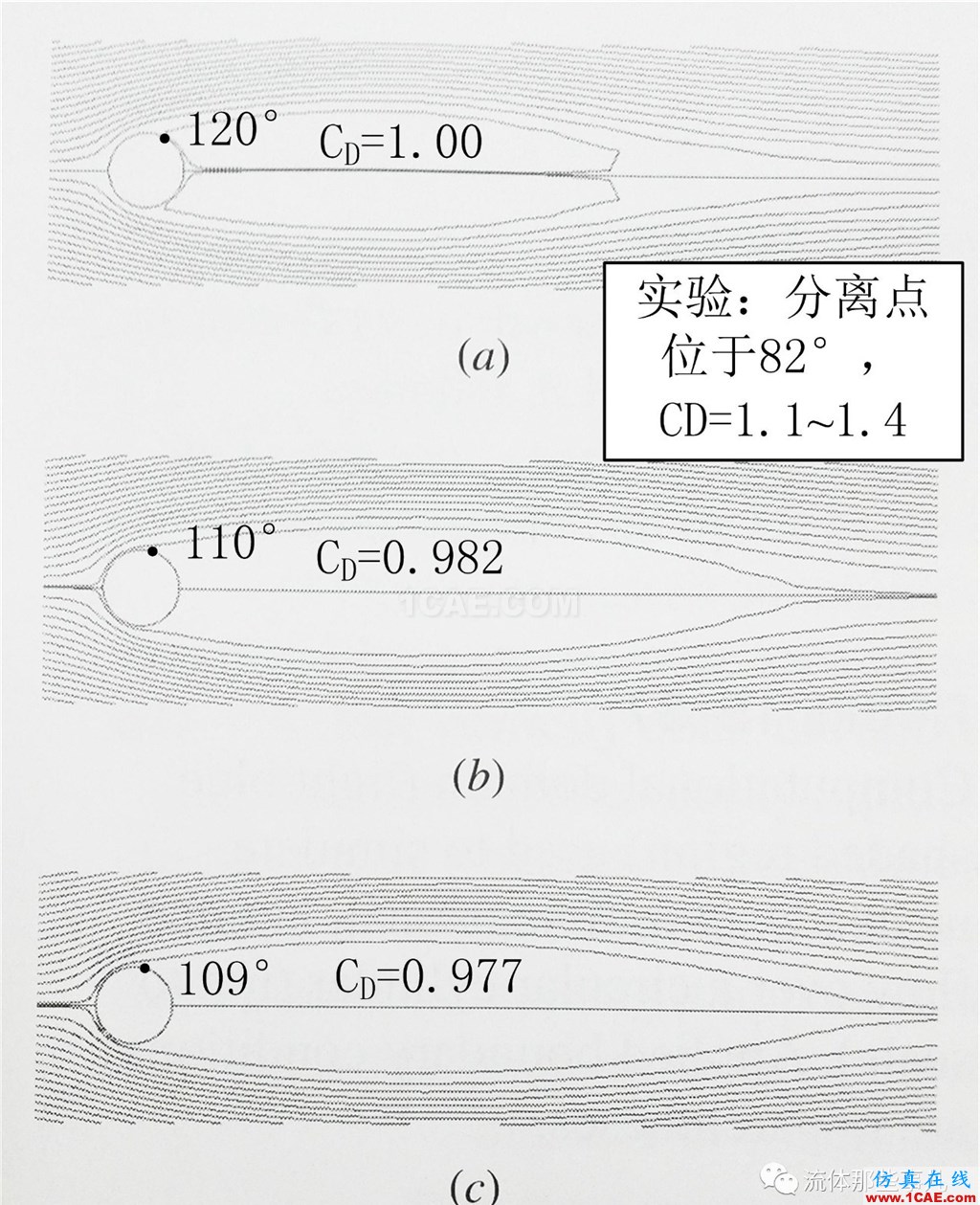
圖6 Re=150的流線。(a) 粗網格;(b) 中等網格;(c) 細網格

(復制自文獻[2])

顯然,數值模擬結果并不符合實際。實驗表明分離點位于圓柱最高點前方,在82°的位置,而數值模擬的結果中,分離點位于圓柱最高點后方,在約109°的位置。此外,數值模擬算出的阻力系數也比實驗值小。

對于Re=104,實驗結果表明圓柱前部的附著邊界層是層流的,分離點也位于82°的位置,但是,圓柱的尾跡是湍流的;實驗測得的阻力系數為1.15。這個雷諾數下使用k-ε湍流模型計算;入口的湍流度設為10%,湍流長度尺度設為圓柱直徑的一半。圖7是三種不同密度網格的計算結果(流線圖);三種密度的網格的計算收斂性都很好。對于圖7(a)的粗網格的結果,邊界層分離點在圓柱頂部后方很遠的地方(140°處),算出的阻力系數只有0.647,幾乎比實驗值小了一半。對于圖7(b)的中等網格的結果,分離點前移到104°的位置,阻力系數增加到0.742——雖然離實驗值近了一些,但是仍然顯著小于實驗值。對于圖7(c)的細網格的結果,與中等網格的結果非常相似,阻力系數為0.753,分離點位于102°的位置。可以看出,這次數值模擬結果仍然不符合實際;分離點的位置與實驗不符,阻力系數也顯著小于實驗值。

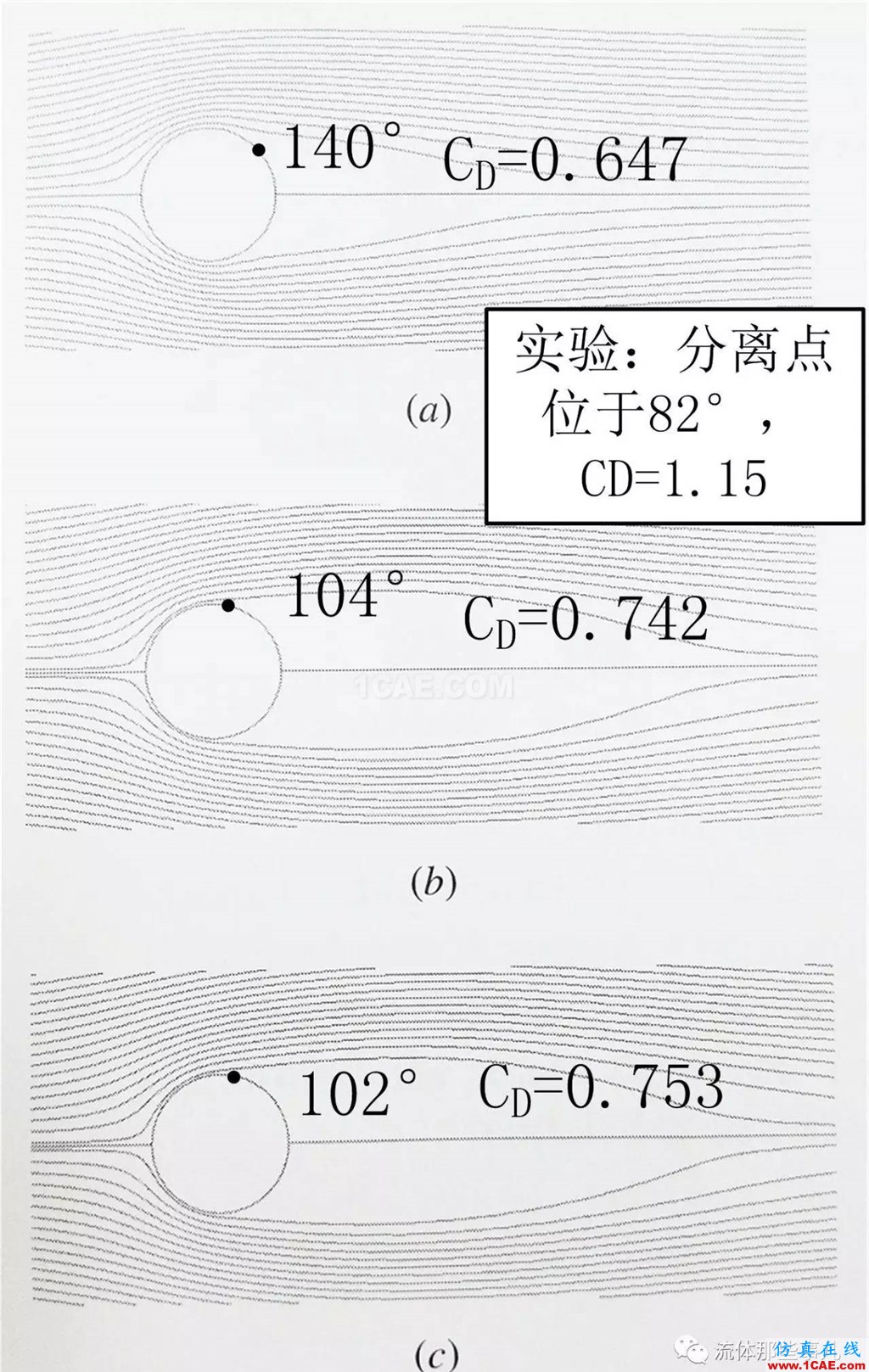
圖7 Re=104的流線。 (a) 粗網格;(b) 中等網格;(c) 細網格

(復制自文獻[2])

對于Re=107,實驗結果表明圓柱表面的附著邊界層是湍流的(頭部駐點附近除外),尾跡當然也是湍流的;分離點位于圓柱最高點后方,在120°的位置(圖5(b));阻力系數為0.7。這個雷諾數的流動同樣使用k-ε湍流模型計算。網格的密度與前述的細網格相似,但是在壁面附近按照湍流模擬中近壁面網格的要求進行加密(因為這時雷諾數很高,邊界層很薄);與Re=104時一樣,入口的湍流度設為10%,湍流長度尺度設為圓柱直徑的一半。不幸的是,算出的阻力系數只有0.262——比實驗值的一半還要小。按計算結果畫出的流線如圖8所示;算出的分離點位于129°的位置,雖然與實驗值同處于圓柱最高點后方,但是與實驗值相比要往下游一些。

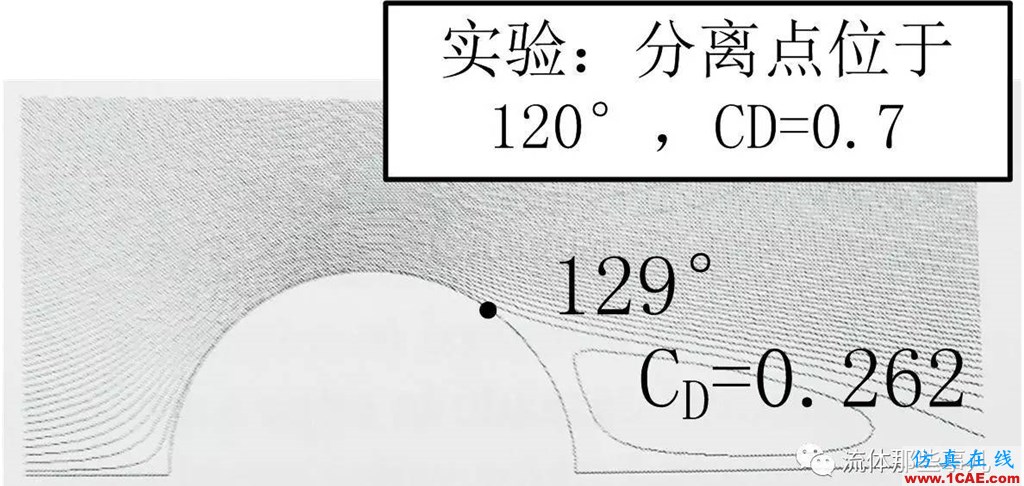
圖8 Re=107的流線。數值模擬的結果。(復制自文獻[2])

Re=150,104和107這三種情形分別代表了圓柱分離流動的三種最典型的流態,即“層流邊界層—層流尾跡”、“層流邊界層—湍流尾跡”以及“湍流邊界層—湍流尾跡”。不幸的是,三種流態的數值模擬都以徹底失敗告終。

實際上,對于Re=150的情形,圓柱尾跡中存在非定常的卡門渦街,附著渦交替地從圓柱的兩側脫落。而在計算模型中,根據圓柱的幾何對稱性天真地將計算域設為實際流動區域的一半,并在x軸上應用了對稱邊界條件;再者,計算過程中使用了定常的求解器;這些都是違背實際發生的物理機制的。計算結果表明,如果將計算域擴展到整個流動區域,并且使用非定常求解算法,就可以算出非定常的卡門渦街來,對算得的非定常阻力系數取時間平均之后,約為1.14,這時就落在實驗值的范圍(1.1~1.4)里面了。計算值接近實驗值范圍下限的原因可能是計算時采用了二維模型,使得任何傾斜的渦脫落或者其它三維不均勻性都被抑制了。

對于Re=104的情形,我們為了模擬湍流尾跡,使用了湍流模型進行計算。但是,實驗結果表明,圓柱表面的邊界層是層流的,這是計算結果不符合實際的重要原因。在我們的計算結果中,邊界層的分離點位于>90°的位置;實際上只有當圓柱表面為湍流邊界層時,分離點才會移動到這樣的位置。總之,層流/湍流混合流動對于數值模擬來說,仍然是非常困難的問題。另外,實驗表明這個雷諾數下尾跡是非定常的,而我們使用定常求解算法并在x軸使用了對稱邊界條件,這也是不符合實際的。

對于Re=107的情形,實際上圓柱下游存在湍流的卡門渦街,而我們使用定常求解算法并在x軸使用了對稱邊界條件,這是不符合實際的。

對Re=104這一類“層流邊界層—湍流尾跡”的流態以及Re=107這一類“湍流邊界層—湍流尾跡”的流態,要采用更細致的模擬方法才能得到合理的結果。例如,文獻[3]采用了二維非定常RANS和三維DES對這兩種流態進行了模擬(見注1),其結果表明,對于后一種流態,兩種方法都能得到比較合理的結果;而對于前一種流態,只有三維DES才能得到合理的結果。

順便說一句,從圖2可以看出,Re=2.5×105時阻力系數突然下降。層流邊界層分離點位置與湍流邊界層分離點位置的截然不同,正是造成這時阻力系數突然下降的原因。當雷諾數超過此值時,邊界層從層流轉捩為湍流,由于湍流邊界層對抗分離的能力比層流的強,所以分離點突然從<90°的位置移動到>90°的位置,使得尾跡顯著變窄,壓差阻力大大降低。這就是著名的圓柱繞流“阻力危機”(drag crisis)現象。所謂的危機并不是流動現象有什么很壞的影響,而是說這個現象使傳統的流體力學理論受到了挑戰,學術界出現了危機[4]。

從這幾個例子還可以看出,要正確地模擬流動問題,必須對流動的物理機制有一定的認識;不懂物理機制而盲目地進行計算,常常會得到錯誤的結果。

未經許可,不得轉載

參考文獻

[1]莊禮賢, 尹協遠, 馬暉揚. 流體力學. 第二版. 中國科學技術大學出版社,2009

[2] Yunus A. ?engel, John M. Cimbala. Fluid Mechanics: fundamental and applications. McGraw-Hill, 2014

[3] ANDREI TRAVIN, MICHAEL SHUR, MICHAEL STRELETS and PHILIPPE SPALART. Detached-eddy simulations Past a Circular Cylinder. Flow, Turbulence and Combustion, 63, 1999

[4] 王洪偉. 我說理解的流體力學. 北京:國防工業出版社,2014

注1:RANS是“雷諾平均方法”(Reynolds averaged Navier-Stokes),即我們在商業軟件中常用的湍流模型;DES是“脫體渦數值模擬”,即在流動附著于壁面的區域采用RANS,在其它區域自動轉變為大渦模擬。

轉自公眾號:流體那些事兒

開放分享：優質有限元技術文章,助你自學成才